In the previous post we defined the True Positive Rate (TPR) and False Positive Rate (FPR) in the open world as follows:
TPR = TP / monitored elements = TP / (TP + FN + FPP)FPR = FP / non-monitored elements = (FPP + FNP) / (TN + FNP)
TPR captures the probability that an access to a monitored page is correctly detect, while FPR captures the probability of false alarms (sort of). We also took a classifier-centric view of the different outcomes of classifier output:
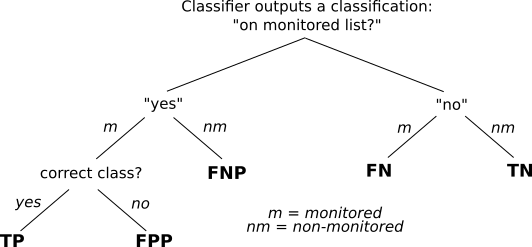
Next, we look closer at the open-world setting and why at least FPR might be less useful.
The base rate fallacy
The base rate fallacy is a common failure of reasoning related to failing to take into account the context of information. Instead of repeating clear examples, we’ll directly dive into the implications for WF-attacks. The context that is often not fully taken into account for WF-attacks is the size of the open world. There are, without exaggeration, billions of webpages on the Internet. Note that, technically, each dynamically generated page on a website like Google, Facebook, or Twitter is a page on its own. Unthinkable complexity. If an attacker has a monitored list of webpages, the probability that a client will visit one of the relatively few webpages monitored by the attacker is presumably really low. This probability is known as the base rate.
What the base rate does to the equation is that it turns any remotely sized FPR (that is primarily due to FNP, i.e., classifying a non-monitored page as monitored) into a WF attack that “cries wolf” even at a seemingly small FPR like 2%. The relationship between the base rate and FPR is therefore a key consideration when evaluating the impact of WF-attacks in the real world [0,1].
Precision
To better take into account the prior information in the open world, precision is a metric that can be used instead of FPR. Precision is defined as the number of true positives divided by the number of positive test outcomes [1]. By “true positives” we mean just that: when the classifier correctly classifies a page (TP). By “positive test outcomes” we mean every time the classifier’s output indicates that an element is a monitored page (gives a positive outcome). In the open-world setting, this is TP + FPP + FNP: the correctly classified elements (TP), the wrongly classified elements on the monitored list (FPP), and the wrongly classified elements for non-monitored pages (FNP). The end result is that we define precision as precision = TP / (TP + FPP + FNP).
Now imagine the most precise classifier which has precision 1. This implies that FPP = FNP = 0. A classifier becomes less precise in two cases:
- The classifier confuses different pages on the monitored list, resulting in an increased FPP.
- The classifier mistakingly classifies non-monitored pages as monitored, resulting in an increased FNP.
It is primarily for the second case that precision becomes a better metric for the open-world setting than FPR. As the number of non-monitored pages increases, the precision goes strictly down if the classifier fails to distinguish between monitored and non-monitored pages. FPR, on the other hand, is defined as FPR = (FPP + FNP) / (TN + FNP). FNP needs to dominate FPP and TN for FPR to get high. With a small base rate, per definition, FPP should be small and for a good classifier (per definition) TN will be large, leading to a small FPR. So, a good classifier will have low FPR, but a low FPR does not necessarily mean the classifier is good, because it might simply be reasonably good at determining TN which will dominate FNP.
Recall
Recall is a metric used in conjunction with precision and is the same as TPR, such that recall = TPR = TP / (TP + FN + FPP). While precision is focused on when the classifier gives a positive classification (TP, FPP and FNP on the left-hand side of the classification figure in the top of this post), recall is focused on when the client visits a monitored page (TP, FN and FPP in the classification figure). Precision captures how relevant a positive from the classifier is, while recall tells us how many out of all visits by the client the classifier accurately detects. The figure below, modified from a relevant Wikipedia article, maps the key concepts. Note that the figure below is made for binary classification, such that FPP cannot be accurately mapped since it represents classification of the wrong class for a positive relevant element. For recall, FPP is relevant because it’s a monitored page the client visits. For precision, FPP is a(n incorrect) positive test outcome.
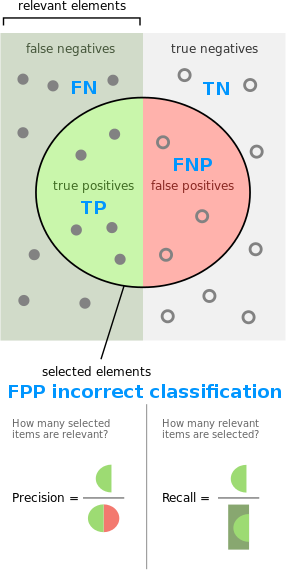
Wrapping up
The open-world setting for WF attacks is complex to reason about. Recent work focus on the base rate fallacy and its importance when evaluating the real-world impact of WF-attacks. Worth noting is that the base rate depends largely on user behavior, which (at least a passive attacker) has no control over. Another important consideration is websites vs webpages. Using state-of-the-art attacks in large open-world settings, Panchenko et al. in recent work concludes that the attacks might realistically be able to identify websites, while webpages not so much [1]. Below is one figure from their paper, showing the precision and recall for classifying websites on the left and webpages on the right. Note that background size is the number of pages in the open world.
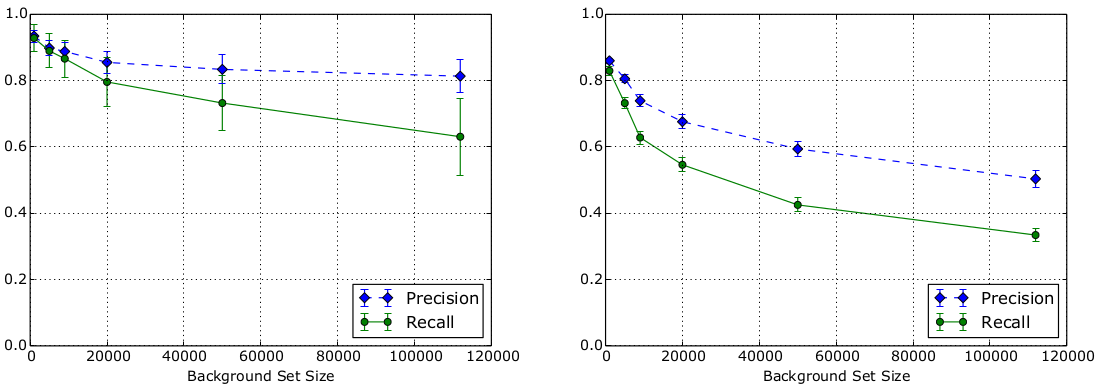
On a depressingly related note, read about NSA’s SKYNET program and how a “completely bullshit” and “ridiculously optimistic” machine learning algorithm may be part of killing thousands of innocent people (thanks Toke).
Sources
- [0] Section 2.2.2 in Tao Wang’s PhD thesis.
- [1] Website Fingerprinting at Internet Scale.
- [2] A Critical Analysis of Website Fingerprinting Attacks
- [3] WTF-PAD: Toward an Efficient Website Fingerprinting Defense for Tor
- Precision and recall image from Wikipedia by Walber (CC BY-SA 4.0).
- Experiment results from websites vs webpages from [1].